Gambling has always been a game of chance, and slot machines are no exception. The allure of hitting the jackpot with a single spin is what keeps players coming back. But how hard is it really to beat a fair gambling slot machine? In this blog post, we will explore the mathematics behind slot machines and why the odds are always in favor of the house.
Figure 1. Image of a casino crash game in action.
#What is a gambling Crash game?
Crash is one of the most popular provably fair game. There are different variants of the game available at different casinos but they all have a similar manner in which it works. A rocket starts going up and will crash at a particular multiplier, and players need to cash their bets before the rocket crashes down.
It is a thrilling experience to play a crash game because it requires a good balance of greed and panic. If you cash out too early, you may regret watching the rocket go high, while if you get greedy and the rocket crashes, you will lose all the potential profits.
#The Concept of Fairness
A fair gambling slot machine is one where the outcomes are truly random and each spin is independent of the previous ones. This means that the probability of hitting a winning combination is the same on every spin. Casinos use Random Number Generators (RNGs) to ensure this fairness.
#The House Edge
The house edge is the mathematical advantage that the casino has over the players. It is the percentage of each bet that the casino expects to keep over the long run. For example, if a slot machine has a house edge of 5%, it means that for every $100 wagered, the casino expects to keep $5. This edge is built into the game and ensures that the casino will always make a profit in the long run.
#The Role of Variance
Variance is a measure of how much the outcomes of a game can vary. In slot machines, high variance means that the payouts are less frequent but larger, while low variance means that the payouts are more frequent but smaller. High variance games can be more exciting, but they also come with a higher risk.
#The Mathematics Behind Slot Machines
Slot machines use complex algorithms to determine the outcomes of each spin. These algorithms take into account the number of symbols on each reel, the number of reels, and the paytable. The probability of hitting a winning combination is calculated using these factors.
#Example Calculation
Let’s consider a simple slot machine with 3 reels and 10 symbols on each reel. The probability of hitting a specific symbol on one reel is 1/10. The probability of hitting the same symbol on all three reels is:
(1/10) * (1/10) * (1/10) = 1/1000
This means that the odds of hitting this combination are 1 in 1000.
#Constants
MULTIPLIER_MIN = 1.00
MULTIPLIER_MAX = 1000000000.00
FORMULA_MIN = 1
FORMULA_MAX = 1000000000
M_STEP = 0.01
M_RECOVER = 2
NUM_SAMPLES = 100000
NUM_MARTINGALE_TESTS = 64
#Functions
def calculate_ev(multiplier):
return ((1/33) + (32/33)*(.01 + .99*(1 - 1/(sweet_spots[0]-.01))))*-1 + (sweet_spots[0]-1)*(1 - ((1/33) + (32/33)*(.01 + .99*(1 - 1/(multiplier-.01)))))
def contiguous_regions(condition):
"""Finds contiguous True regions of the boolean array "condition". Returns
a 2D array where the first column is the start index of the region and the
second column is the end index."""
d = np.diff(condition)
idx, = d.nonzero()
idx += 1
if condition[0]:
idx = np.r_[0, idx]
if condition[-1]:
idx = np.r_[idx, condition.size]
idx.shape = (-1,2)
return idx
f = lambda x: 1.00 if np.random.randint(low=FORMULA_MIN, high=FORMULA_MAX) < (1000000000 * 0.06) else (1000000000 / np.random.randint(low=FORMULA_MIN, high=FORMULA_MAX))
def get_segs(arr, cond):
segs = []
for start, stop in contiguous_regions(cond):
segment = arr[start:stop]
segs.append(stop - start)
return np.array(segs)
def count_neg(arr, m):
negatives = []
in_a_row = 0
for multiplier in arr:
if multiplier < m:
in_a_row += 1
else:
in_a_row = 0
negatives.append(in_a_row)
return np.array(negatives)
#Generating Samples
np.random.seed(0)
results = np.array(list(map(f, np.empty(NUM_SAMPLES))))
#Visualizations
#Histogram of Game Results
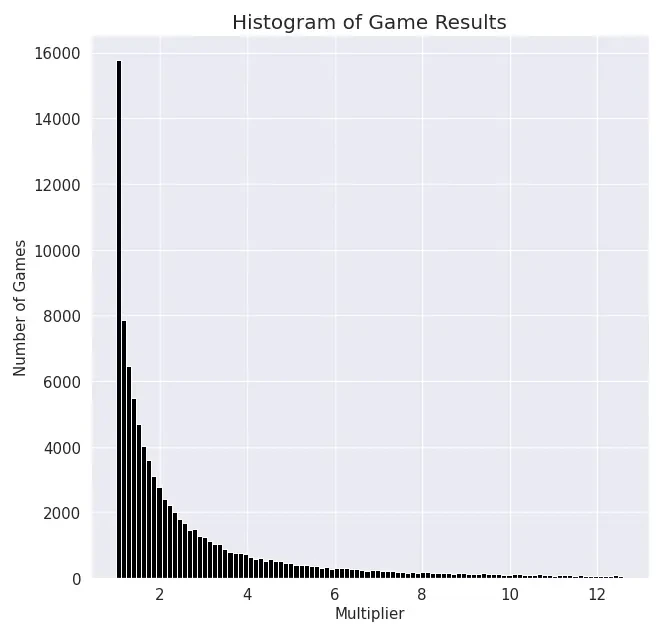
Figure 2. Histogram of Game Results.
#Expected Value by Multiplier
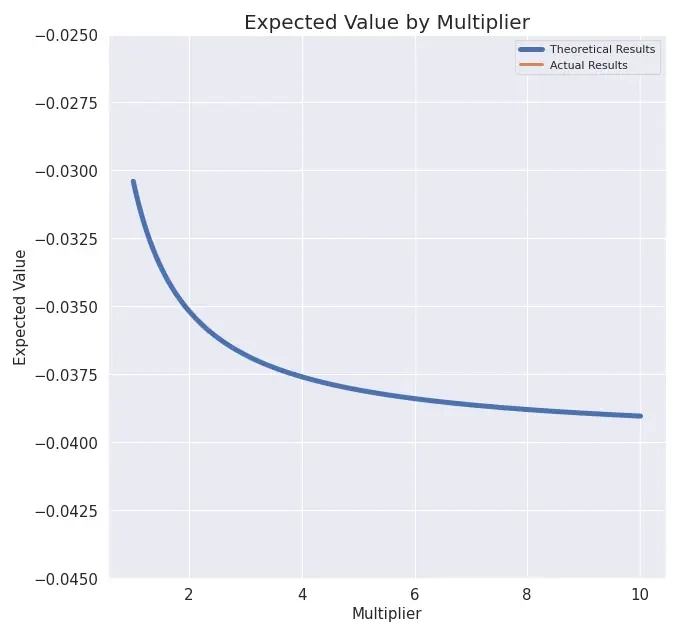
Figure 3. Expected Value by Multiplier.
#Martingale Test
The code:
if np.median(results) > MULTIPLIER_MIN:
print("Mean")
for i in range(1, NUM_MARTINGALE_TESTS):
print("P of Losing %d Game (%.2fx) in-Row: %.4f (%.2f%%)" % (i, (results.mean() - M_STEP), (m_mean_neg >= i).mean(), (m_mean_neg >= i).mean()*100))
print("Median")
for i in range(1, NUM_MARTINGALE_TESTS):
print("P of Losing %d Game (%.2fx) in-Row: %.4f (%.2f%%)" % (i, (np.median(results) - M_STEP), (m_median_neg >= i).mean(), (m_median_neg >= i).mean()*100))
print("Recover")
for i in range(1, NUM_MARTINGALE_TESTS):
print("P of Losing %d Game (%.2fx) in-Row: %.4f (%.2f%%)" % (i, (M_RECOVER-M_STEP), (m_recover_neg >= i).mean(), (m_recover_neg >= i).mean()*100))
The results:
Mean = Multiplier of x 12.59 (1259%)
P of Losing 1 Game (12.59x) in-Row: 0.9257 (92.58%)
P of Losing 2 Game (12.59x) in-Row: 0.8568 (85.68%)
P of Losing 3 Game (12.59x) in-Row: 0.7925 (79.25%)
P of Losing 4 Game (12.59x) in-Row: 0.7332 (73.32%)
P of Losing 5 Game (12.59x) in-Row: 0.6785 (67.86%)
P of Losing 6 Game (12.59x) in-Row: 0.6277 (62.77%)
P of Losing 7 Game (12.59x) in-Row: 0.5808 (58.08%)
P of Losing 8 Game (12.59x) in-Row: 0.5373 (53.73%)
P of Losing 9 Game (12.59x) in-Row: 0.4973 (49.73%)
P of Losing 10 Game (12.59x) in-Row: 0.4603 (46.03%)
P of Losing 11 Game (12.59x) in-Row: 0.4263 (42.63%)
P of Losing 12 Game (12.59x) in-Row: 0.3946 (39.46%)
P of Losing 13 Game (12.59x) in-Row: 0.3654 (36.54%)
P of Losing 14 Game (12.59x) in-Row: 0.3384 (33.84%)
P of Losing 15 Game (12.59x) in-Row: 0.3136 (31.36%)
P of Losing 16 Game (12.59x) in-Row: 0.2906 (29.06%)
P of Losing 17 Game (12.59x) in-Row: 0.2693 (26.93%)
P of Losing 18 Game (12.59x) in-Row: 0.2495 (24.95%)
P of Losing 19 Game (12.59x) in-Row: 0.2311 (23.11%)
P of Losing 20 Game (12.59x) in-Row: 0.2142 (21.42%)
P of Losing 21 Game (12.59x) in-Row: 0.1985 (19.85%)
P of Losing 22 Game (12.59x) in-Row: 0.1839 (18.39%)
P of Losing 23 Game (12.59x) in-Row: 0.1704 (17.04%)
P of Losing 24 Game (12.59x) in-Row: 0.1580 (15.80%)
P of Losing 25 Game (12.59x) in-Row: 0.1466 (14.66%)
P of Losing 26 Game (12.59x) in-Row: 0.1358 (13.58%)
P of Losing 27 Game (12.59x) in-Row: 0.1258 (12.58%)
P of Losing 28 Game (12.59x) in-Row: 0.1166 (11.66%)
P of Losing 29 Game (12.59x) in-Row: 0.1082 (10.82%)
P of Losing 30 Game (12.59x) in-Row: 0.1003 (10.03%)
P of Losing 31 Game (12.59x) in-Row: 0.0930 (9.30%)
P of Losing 32 Game (12.59x) in-Row: 0.0863 (8.63%)
P of Losing 33 Game (12.59x) in-Row: 0.0802 (8.02%)
P of Losing 34 Game (12.59x) in-Row: 0.0746 (7.46%)
P of Losing 35 Game (12.59x) in-Row: 0.0693 (6.93%)
P of Losing 36 Game (12.59x) in-Row: 0.0643 (6.43%)
P of Losing 37 Game (12.59x) in-Row: 0.0597 (5.96%)
P of Losing 38 Game (12.59x) in-Row: 0.0553 (5.53%)
P of Losing 39 Game (12.59x) in-Row: 0.0513 (5.13%)
P of Losing 40 Game (12.59x) in-Row: 0.0476 (4.76%)
P of Losing 41 Game (12.59x) in-Row: 0.0440 (4.40%)
P of Losing 42 Game (12.59x) in-Row: 0.0408 (4.08%)
P of Losing 43 Game (12.59x) in-Row: 0.0379 (3.79%)
P of Losing 44 Game (12.59x) in-Row: 0.0352 (3.52%)
P of Losing 45 Game (12.59x) in-Row: 0.0327 (3.27%)
P of Losing 46 Game (12.59x) in-Row: 0.0305 (3.05%)
P of Losing 47 Game (12.59x) in-Row: 0.0284 (2.84%)
P of Losing 48 Game (12.59x) in-Row: 0.0265 (2.65%)
P of Losing 49 Game (12.59x) in-Row: 0.0248 (2.48%)
P of Losing 50 Game (12.59x) in-Row: 0.0231 (2.31%)
P of Losing 51 Game (12.59x) in-Row: 0.0216 (2.16%)
P of Losing 52 Game (12.59x) in-Row: 0.0202 (2.02%)
P of Losing 53 Game (12.59x) in-Row: 0.0188 (1.88%)
P of Losing 54 Game (12.59x) in-Row: 0.0176 (1.76%)
P of Losing 55 Game (12.59x) in-Row: 0.0164 (1.64%)
P of Losing 56 Game (12.59x) in-Row: 0.0153 (1.53%)
P of Losing 57 Game (12.59x) in-Row: 0.0143 (1.43%)
P of Losing 58 Game (12.59x) in-Row: 0.0133 (1.33%)
P of Losing 59 Game (12.59x) in-Row: 0.0124 (1.24%)
P of Losing 60 Game (12.59x) in-Row: 0.0115 (1.15%)
P of Losing 61 Game (12.59x) in-Row: 0.0107 (1.07%)
P of Losing 62 Game (12.59x) in-Row: 0.0100 (1.00%)
P of Losing 63 Game (12.59x) in-Row: 0.0094 (0.94%)
Median = Multiplier of x 1.88 (188%)
P of Losing 1 Game (1.88x) in-Row: 0.4973 (49.73%)
P of Losing 2 Game (1.88x) in-Row: 0.2485 (24.85%)
P of Losing 3 Game (1.88x) in-Row: 0.1236 (12.36%)
P of Losing 4 Game (1.88x) in-Row: 0.0620 (6.20%)
P of Losing 5 Game (1.88x) in-Row: 0.0316 (3.16%)
P of Losing 6 Game (1.88x) in-Row: 0.0162 (1.62%)
P of Losing 7 Game (1.88x) in-Row: 0.0083 (0.83%)
P of Losing 8 Game (1.88x) in-Row: 0.0043 (0.43%)
P of Losing 9 Game (1.88x) in-Row: 0.0022 (0.21%)
P of Losing 10 Game (1.88x) in-Row: 0.0010 (0.10%)
P of Losing 11 Game (1.88x) in-Row: 0.0004 (0.04%)
P of Losing 12 Game (1.88x) in-Row: 0.0002 (0.02%)
P of Losing 13 Game (1.88x) in-Row: 0.0001 (0.01%)
P of Losing 14 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 15 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 16 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 17 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 18 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 19 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 20 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 21 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 22 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 23 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 24 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 25 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 26 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 27 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 28 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 29 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 30 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 31 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 32 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 33 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 34 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 35 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 36 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 37 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 38 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 39 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 40 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 41 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 42 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 43 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 44 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 45 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 46 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 47 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 48 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 49 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 50 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 51 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 52 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 53 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 54 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 55 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 56 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 57 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 58 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 59 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 60 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 61 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 62 Game (1.88x) in-Row: 0.0000 (0.00%)
P of Losing 63 Game (1.88x) in-Row: 0.0000 (0.00%)
Recover = Multiplier of x 1.99 (199%)
P of Losing 1 Game (1.99x) in-Row: 0.5274 (52.74%)
P of Losing 2 Game (1.99x) in-Row: 0.2792 (27.93%)
P of Losing 3 Game (1.99x) in-Row: 0.1477 (14.77%)
P of Losing 4 Game (1.99x) in-Row: 0.0781 (7.81%)
P of Losing 5 Game (1.99x) in-Row: 0.0418 (4.18%)
P of Losing 6 Game (1.99x) in-Row: 0.0224 (2.24%)
P of Losing 7 Game (1.99x) in-Row: 0.0120 (1.20%)
P of Losing 8 Game (1.99x) in-Row: 0.0064 (0.64%)
P of Losing 9 Game (1.99x) in-Row: 0.0034 (0.34%)
P of Losing 10 Game (1.99x) in-Row: 0.0017 (0.17%)
P of Losing 11 Game (1.99x) in-Row: 0.0008 (0.08%)
P of Losing 12 Game (1.99x) in-Row: 0.0004 (0.04%)
P of Losing 13 Game (1.99x) in-Row: 0.0002 (0.02%)
P of Losing 14 Game (1.99x) in-Row: 0.0001 (0.01%)
P of Losing 15 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 16 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 17 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 18 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 19 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 20 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 21 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 22 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 23 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 24 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 25 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 26 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 27 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 28 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 29 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 30 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 31 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 32 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 33 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 34 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 35 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 36 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 37 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 38 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 39 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 40 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 41 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 42 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 43 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 44 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 45 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 46 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 47 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 48 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 49 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 50 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 51 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 52 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 53 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 54 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 55 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 56 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 57 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 58 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 59 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 60 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 61 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 62 Game (1.99x) in-Row: 0.0000 (0.00%)
P of Losing 63 Game (1.99x) in-Row: 0.0000 (0.00%)
#Strategies to Beat Slot Machines
Be aware, many players believe that they can develop strategies to beat slot machines. However, because the outcomes are random and each spin is independent, there is no guaranteed way to win. Some common strategies include:
- Betting the maximum: Some slot machines offer higher payouts for maximum bets.
- Choosing high RTP machines: Return to Player (RTP) is the percentage of wagered money that a slot machine will pay back to players over time. Choosing machines with higher RTP can increase your chances of winning.
- Managing your bankroll: Setting limits on how much you are willing to spend and sticking to them can help you avoid losing more money than you can afford.
#Conclusion
Beating a fair gambling slot machine is extremely difficult due to the built-in house edge and the randomness of the outcomes. While there are strategies that can increase your chances of winning, there is no foolproof way to guarantee a win. The best approach is to play responsibly and enjoy the game for what it is – a game of chance.